流體動力學問題剖析
發(fā)布日期: 2018-4-12
本節(jié)主要討論流體在運動時的運動規(guī)律、能量轉換以及運動流體對固體壁面的作用力和發(fā)作用力等問題,具體要介紹三個基本方程式及連續(xù)方程、能量方程和動量方程。
不過對液壓技術來說,讓人感興趣的應該是整個流體在空間某特定點處或特定區(qū)域內的平均運動情況。此外,運動流體的狀態(tài)還與流體的溫度、粘度等參數都有聯(lián)系。為了簡化條件便于分析,一般都假設在等溫的條件下(因而可把粘度看作是常量,密度只與壓強有關)來討論流體的運動情況。
一、基礎概念
在推導流體運動的三個基本方程之前,必須弄清有關流體運動時的一些主要基礎概念。
(一)理想流體、恒定運動和一維運動實際流體體具有粘性,研究流體運動時必須考慮粘性的影響。但由于這個問題很復雜,所以開始分析時可以假設流體體沒有粘性,然后再考慮粘性的作用并通過實驗驗證等辦法對理想化的結論進行補充或修正。這種方法同樣可以用來處理流體的可壓縮性問題。一般把既無粘性又不可壓縮的假想流體稱為理想流體。
流體運動時,如流體中任何一點的壓強、速度和密度都不隨時間而變化,便稱流體是在作恒定運動;反之,只要壓強、速度或密度中有一個參數隨時間變化,則流體的運動被稱為非恒定運動。研究液壓系統(tǒng)穩(wěn)態(tài)性能時,可以認為流體作恒定運動;但在研究其動態(tài)性能時,則必須按非恒定運動來考慮。
當流體整個作線形運動時,稱為一維運動;當作平面或空間運動時,稱為二維或三維運動。一維運動最簡單,但是嚴格意義上的一維運動要求液流截面上各點處的速度矢量完全相同,這種情況在現實中極為少見。通常把封閉容器內流體的運動按一維運動處理,再用實驗數據來修正其結果,液壓傳動中對工作介質運動的分析討論就是這樣進行的。
(二)流線、流管和流束
流線是流場中的一條條曲線,它表示在同一瞬時流場中各質點的運動狀態(tài)。流線上每一質點的速度向量與這條曲線相切,因此,流線代表了某一瞬時一群流體質點的流速方向,如下圖1-1所示。在非恒定運動時,由于液流通過空間點的速度隨時間變化,因而流線形狀也隨時間變化;在恒定運動時,流線形狀不隨時間變化。由于流場中每一質點在每一瞬時只能有一個速度,所以流線之間不可能相交,流線也不可能突然轉折,它只能是一條光滑的曲線。
在流場中畫一不屬于流線的任意封閉曲線,沿該封閉曲線上的每一點作流線,由這些流線組成的表面稱為
如圖1-1流線、流管、流束和通流截面
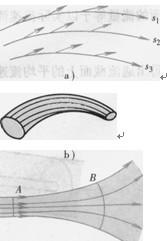
a)流線b)流管c)流束和通流截面
流管(見圖1-2b)。流管內的流線群稱為流束。根據流線不會相交的性質,流管內外的流線均不會穿越流管,故流管與真實管道相似。將流管截面無限縮小趨近于零,便獲得微小流管或微小流束。微小流束截面上各點處的流速可以認為是相等的。
流線彼此平行的運動稱為平行運動;流線間夾角很小,或流線曲率半徑很大的運動稱為緩變運動。平行運動和緩變運動都可以算是一維運動。
(三)通流截面、流量和平均流速
流束中與所有流線正交的截面稱為通流截面,如圖1-2c中的A面和曰面,通流截面上每點處的運動速度都垂直于這個面。
單位時間內流過某通流截面的流體體積稱為流量,常用g表示,即
Q=V/T
式中q-流量,在液壓傳動中流量常用單位為L/min;
V—一流體的體積;
T——流過流體體積y所需的時間。
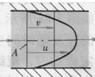
由于實際流體具有粘性,因此流體在管道內運動時,通流截面上各點的流速是不相等的。管壁處的流速為零,管道中心處流速最大,流速分布。若欲求得流經整個通流截面A的流量,可在通流截面A上取一微小流束的截面dA,則通過dA的微小流量為
dq=udA
對上式進行積分,便可得到流經整個通流截面A的流量
q= udA
可見,要求得g的值,必須先知道流速M在整個通流截面A上的分布規(guī)律。實際上這是比較困難的,因為粘性流體流速M在管道中的分布規(guī)律是很復雜的。所以,為方便起見,在液壓傳動中常采用一個假想的平均流速來求流量,并認為流體以平均流速流經通流截面的流量等于以實際流速流過的流量,即
q= udA= vA
由此得出通流截面上的平均流速為
v=q/a


a) b)
流量也可以 用單位時間內流過某通流截面的流體質量來表示,即dq。=pudA及g。=
f pMdA,g。稱為質量流量。
oA
(四)運動流體的壓強
靜止流體內任意點處的壓強在各個方向上都是相等的;可是在運動流體內,由于慣性力和粘性力的影響,任意點處在各個方向上的壓強并不相等,但在數值上相差甚微。當慣性力很小,且把流體當作理想流體時,運動流體內任意點處的壓強在各個方向上的數值仍可以看作是相等的。